蚁群算法与 TSP 问题

lornd

发布于：2021年12月1日

次浏览

TSP 问题

旅行商问题（Travelling Salesman Problem，TSP）：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。

蚁群算法

蚁群算法（Ant Colony Optimization, ACO）是人们受到自然界中蚂蚁在寻找食物过程中发现路径的行为启发而提出的一种算法。因此，要理解蚁群算法，我们需要先理解蚂蚁发现路径的行为。

众所周知，自然界中，蚂蚁之间使用信息素进行通讯。蚂蚁在经过的路径上留下信息素，指引着其他蚂蚁的前进。如下图所示：

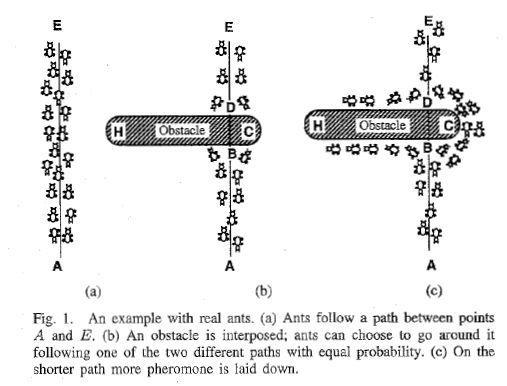
假设蚂蚁巢位于 A 点，食物位于 E 点。蚂蚁从 A 点出发，到达 E 点取得食物，再携带食物返回 A 点。当 A 点和 E 点之间没有障碍物时，先出发的蚂蚁沿着直线从 A 到 E ，再沿着直线从 E 到 A ，因此蚂蚁留下的所有信息素都在一条直线上，后出发的蚂蚁也都会沿着直线在 A、E 两点之间来回搬运食物。

若 A 点和 E 点之间存在障碍物，蚂蚁先沿着直线前进，在碰到障碍物的时候，先出发的蚂蚁由于没有任何信息素指导，因此随机选择向左或者向右前进，并在对应的路径上留下信息素。因为右边的路径总长度更短，向右走的蚂蚁很快又会返回，导致右边路径信息素的聚集速度要高于左边路径上信息素聚集速度。久而久之，右边路径上信息素的浓度会高于左边路径上信息素的浓度。在这之后到达障碍物前的蚂蚁，由于右边路径上信息素浓度更高，这些蚂蚁会更加倾向于走右边的路径，继续为右边的路径带来更多的信息素……如此循环下去，最终，右边路径上信息素的浓度会远远高于左边路径上信息素的浓度，所有的蚂蚁都会选择右边的路径。

而从宏观上来看，在障碍物处向右走确实是蚂蚁取食的最优路径。受此启发，我们在解决一些问题的时候，也可以人工创造一些“蚂蚁”，让它们去尝试解决这个问题，并在自己解决问题的过程中留下“信息素”，来指导其他“蚂蚁”解决问题，在受影响的蚂蚁（代数）足够多之后，我们便可以找到问题的最优解。而这，就是蚁群算法的起源。

综上，我们可以总结出蚁群算法的核心思想：

1. 为“蚂蚁”分配工作，并让它们去完成工作。
2. “蚂蚁”在解决工作所经过的路径上留下“信息素”。
3. 利用“信息素”指导“蚂蚁”完成工作。
4. 重复上述过程，直到不再能产出更优的完成工作的方式（结果收敛）。

接下来，我们利用上述思想去解决 TSP 问题。

蚁群算法在 TSP 问题中的应用

根据蚁群算法的核心思想，在使用蚁群算法解决问题前，需要先定义三个要素：工作、蚂蚁、信息素。TSP 问题属于路径寻找问题，所以我们可以很直观地套用上文提到的蚂蚁觅食的例子。我们放若干只蚂蚁到这些城市中，分别让它们随机在城市之间走出一条回路，并留下信息素指导后代蚂蚁，后代蚂蚁根据信息素去寻找更优的方式……重复上述过程，直到结果收敛。

对于一只蚂蚁，让其随机在城市之间走出一条回路是容易实现的。因此我们的核心问题就变成了对于信息素的处理：如何让蚂蚁留下信息素？如何让蚂蚁根据信息素寻找更优的路径？

基本假设

为了方便后续的讨论，我们先进行一些基本假设：

1. 一共有 $n$ 座城市，第 $i$ 座城市与第 $j$ 座城市之间的距离为 $d_{ij}$。
2. 蚂蚁之间采用隔代影响的方式：即第 $i$ 代蚂蚁留下的信息素只会对它的后代产生影响，而不会对与它同代的蚂蚁产生影响。
3. 每一代的蚂蚁的数量均为 $m$ 只。

如何让蚂蚁留下信息素

我们假设每一只蚂蚁在经过一条路径时，都会在这条路径上均匀撒下量为 $Q$ 的信息素。那么当路径长度为$L$时，这条路径上的信息素浓度就会增加$\Delta P = \dfrac{Q}{L}$。当$Q$一定时，$L$越小，$\Delta P$就会越大，这与我们在蚂蚁觅食的例子中所获得的经验是相近的——越短的路径上，信息素的浓度就会增加得越快。

因此，如果假设$p_{ij}(t)$表示第$t$代蚂蚁开始寻找路径时，城市$i$、$j$之间路径上的信息素的浓度，$\Delta P_{ij}(t)$表示第$t$代蚂蚁在城市$i$、$j$之间路径上所产生的信息素的增量，那么有：

$p_{ij}(t + 1) = p_{ij}(t) + \Delta p_{ij}(t)$

对于$\Delta p_{ij}(t)$，则与第$t$代蚂蚁中走了城市$i$、$j$之间的路径的蚂蚁的数量、城市$i$、$j$之间路径的长度、蚂蚁从城市$i$到城市$j$一路上所留下的信息素的量等因素有关。我们假设蚂蚁在任何两座城市之间运动，所留下的信息素的量均为$Q$，那么就有：

$\Delta p_{ij}(t) = m_{ij}(t) \dfrac{Q}{d_{ij}}$

其中$m_{ij}(t)$表示第$t$代蚂蚁中经过了城市$i$、$j$之间的路径的蚂蚁的数量。

另外，在实际情况中，分布在路径上的信息素会随着时间的流逝而挥发，为了模拟这一过程，我们假设每经过一代，每一条路径上就会挥发掉$\rho$的信息素（$0 < \rho < 1$）。那么，信息素的更新公式修正为如下：

$p_{ij}(t + 1) = (1 - \rho)\ p_{ij}(t) + \Delta p_{ij}(t)$

如何让蚂蚁根据信息素寻找更优的路径

假设第$t$代的某一只蚂蚁当前处在$i$城，下一步它可以去的城市组成了集合$S$，那么一个最直观的想法就是按照每一条路径上信息素浓度比去分配概率，即：

$P_{ij}(t) = \dfrac{p_{ij}(t)}{\sum\limits_{k\in S}p_{ik}(t)}$

为什么会出现集合$S$呢？根据 TSP 问题的定义，在一次回路的寻找中，我们不能重复经过一个城市两次（除了最终回到起点城市），因此我们需要记录哪些城市可以继续走。这个集合$S$被的补集称作为禁忌表，初始$S$为全集（所有城市），在一只蚂蚁的旅行过程中，不断删去蚂蚁经过的城市，最终就能保证蚂蚁一定走了一条没有经过重复城市的回路。

参考文献

1. 蚁群算法 - 维基百科，自由的百科全书
2. 蚁群算法 - 求解 TSP 问题 - 知乎

更新于：2023年9月15日